I am Pengfei Wang (王鹏飞), a Ph.D. candidate at the Interdisciplinary Research Center, Shandong University, where I have been conducting research under the supervision of Prof. Changhe Tu and Prof. Shiqing Xin.
I grew up in Binzhou, Shandong, China. I spent my most memorable time at Beizhen Middle School (class of 2014), where I made some truly great friends.
Warning
Problem: The current name of your GitHub Pages repository ("Solution: Please consider renaming the repository to "
http://".
However, if the current repository name is intended, you can ignore this message by removing "{% include widgets/debug_repo_name.html %}" in index.html.
Action required
Problem: The current root path of this site is "baseurl ("_config.yml.
Solution: Please set the
baseurl in _config.yml to "👩🎓Education
-
Sep. 2024 - PresentShandong University
Interdisciplinary Research Center
Ph.D. Student -
Sep. 2021 - Jun. 2024Shandong University
Interdisciplinary Research Center
Master Student -
Sep. 2017 - Jun. 2021Hunan Normal University
B.S. in Information Science and Engineering
🏆 Honors & Awards
-
The CAST Youth Science and Technology Talent Cultivation Program for Doctoral Students2025
-
National Scholarships2025
-
Best Paper Award (18th International Conference on Geometric Modeling and Processing)2024
News
Selected Publications
(view all )
Swept Volume Computation with Enhanced Geometric Detail Preservation
Pengfei Wang*; Yuexin Yang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
Computer Graphics Forum (CGF). Presented at PG 2025 2025
A novel multi-field tetrahedral framework that inverts motion perspective to robustly compute swept volumes with high geometric fidelity, effectively resolving complex self-intersections where traditional single-field methods fail.
Swept Volume Computation with Enhanced Geometric Detail Preservation
Pengfei Wang*; Yuexin Yang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
A novel multi-field tetrahedral framework that inverts motion perspective to robustly compute swept volumes with high geometric fidelity, effectively resolving complex self-intersections where traditional single-field methods fail.
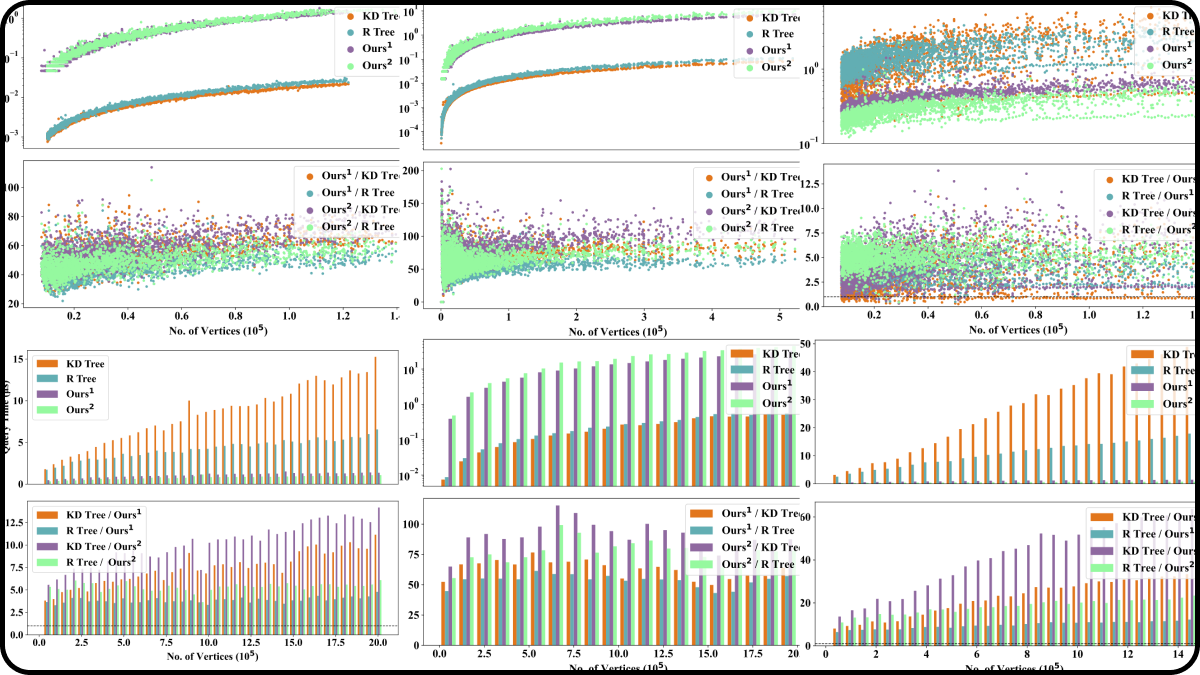
Efficient Nearest Neighbor Search Using Dynamic Programming
Pengfei Wang; Jiantao Song; Shiqing Xin; Shuangmin Chen; Changhe Tu; Wenping Wang; Jiaye Wang.
IEEE Transactions on Pattern Analysis and Machine Intelligence 2025
A novel dynamic programming framework that encodes the incremental evolution of Voronoi diagrams into a DAG to accelerate nearest neighbor search on manifolds and reduce density peak clustering complexity to $O(n \log n)$.
Efficient Nearest Neighbor Search Using Dynamic Programming
Pengfei Wang; Jiantao Song; Shiqing Xin; Shuangmin Chen; Changhe Tu; Wenping Wang; Jiaye Wang.
A novel dynamic programming framework that encodes the incremental evolution of Voronoi diagrams into a DAG to accelerate nearest neighbor search on manifolds and reduce density peak clustering complexity to $O(n \log n)$.
Toward Precise Curve Offsetting Constrained to Parametric Surfaces
Jin Zhao*; Pengfei Wang*; Shuangmin Chen; Jiong Guo; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
Computer-Aided Design (CAD). Presented at SPM 2025 2025
A novel offset computation paradigm that utilizes surface-constrained Voronoi decomposition and intrinsic triangulation to transform complex geodesic tracing into efficient, localized cell-traversal operations on parametric surfaces.
Toward Precise Curve Offsetting Constrained to Parametric Surfaces
Jin Zhao*; Pengfei Wang*; Shuangmin Chen; Jiong Guo; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
A novel offset computation paradigm that utilizes surface-constrained Voronoi decomposition and intrinsic triangulation to transform complex geodesic tracing into efficient, localized cell-traversal operations on parametric surfaces.
Towards Voronoi Diagrams of Surface Patches
Pengfei Wang; Jiantao Song; Lei Wang; Shiqing Xin; Dongming Yan; Shuangmin Chen; Changhe Tu; Wenping Wang.
IEEE Transactions on Visualization and Computer Graphics (TVCG) 2025
A high-fidelity medial axis extraction framework that generalizes Voronoi computation to 4D space via hyperplane cutting within tetrahedral elements, effectively resolving complex surface patch interactions to eliminate discretization artifacts.
Towards Voronoi Diagrams of Surface Patches
Pengfei Wang; Jiantao Song; Lei Wang; Shiqing Xin; Dongming Yan; Shuangmin Chen; Changhe Tu; Wenping Wang.
A high-fidelity medial axis extraction framework that generalizes Voronoi computation to 4D space via hyperplane cutting within tetrahedral elements, effectively resolving complex surface patch interactions to eliminate discretization artifacts.
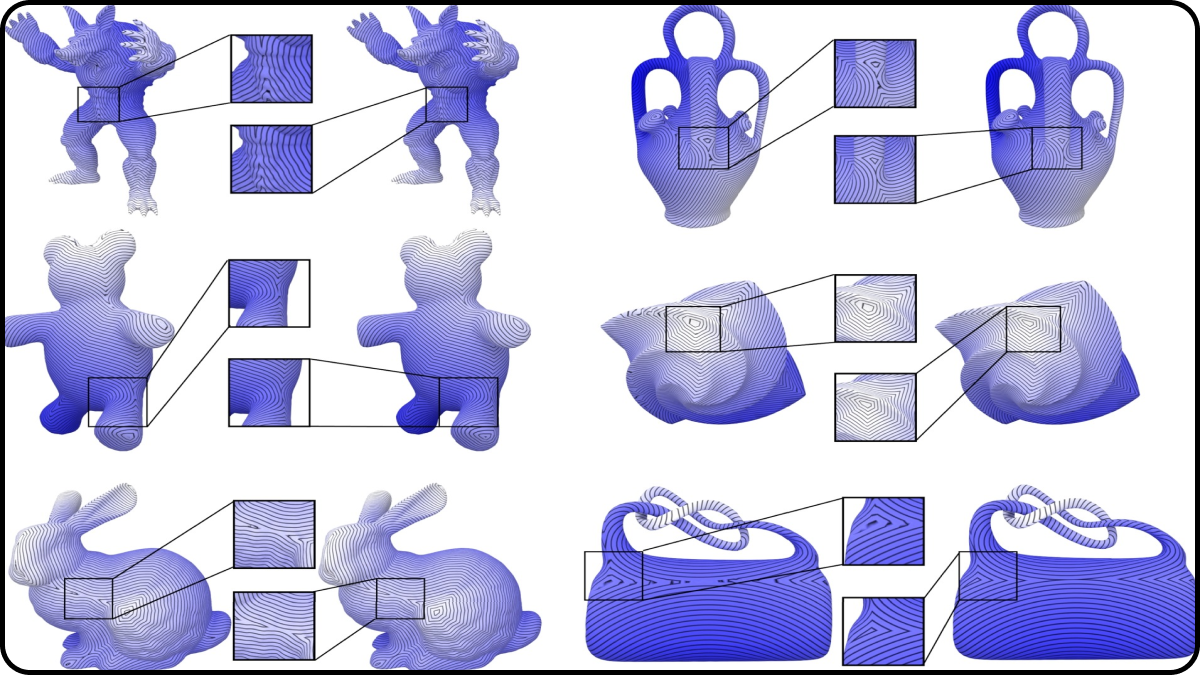
Towards geodesic ridge curve for region-wise linear representation of geodesic distance field
Wei Liu*; Pengfei Wang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Ying He; Wenping Wang. (* equal contribution)
Computer Aided Geometric Design (CAGD). Presented at GMP 2024 2024
A two-stage algorithm to compute the geodesic ridge curve on triangular meshes. By cutting the surface along the dual structure of the shortest path tree and using a fast marching solver on the extended surface, we enable accurate geodesic distance querying and high-fidelity visualization of geodesic iso-lines.
Towards geodesic ridge curve for region-wise linear representation of geodesic distance field
Wei Liu*; Pengfei Wang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Ying He; Wenping Wang. (* equal contribution)
A two-stage algorithm to compute the geodesic ridge curve on triangular meshes. By cutting the surface along the dual structure of the shortest path tree and using a fast marching solver on the extended surface, we enable accurate geodesic distance querying and high-fidelity visualization of geodesic iso-lines.