Under Review


Power Diagram Enhanced Adaptive Isosurface Extraction from Signed Distance Fields
Pengfei Wang; Ziyang Zhang; Wensong Wang; Shuangmin Chen; Lin Lu; Shiqing Xin; Changhe Tu.
Arxiv 2025 2025
A novel isosurface extraction framework that leverages incrementally constructed power diagrams and adaptive sampling to capture intricate geometric and topological details from Signed Distance Fields with minimal computational cost.
Power Diagram Enhanced Adaptive Isosurface Extraction from Signed Distance Fields
Pengfei Wang; Ziyang Zhang; Wensong Wang; Shuangmin Chen; Lin Lu; Shiqing Xin; Changhe Tu.
A novel isosurface extraction framework that leverages incrementally constructed power diagrams and adaptive sampling to capture intricate geometric and topological details from Signed Distance Fields with minimal computational cost.
2025


Swept Volume Computation with Enhanced Geometric Detail Preservation
Pengfei Wang*; Yuexin Yang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
Computer Graphics Forum (CGF). Presented at PG 2025 2025
A novel multi-field tetrahedral framework that inverts motion perspective to robustly compute swept volumes with high geometric fidelity, effectively resolving complex self-intersections where traditional single-field methods fail.
Swept Volume Computation with Enhanced Geometric Detail Preservation
Pengfei Wang*; Yuexin Yang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
A novel multi-field tetrahedral framework that inverts motion perspective to robustly compute swept volumes with high geometric fidelity, effectively resolving complex self-intersections where traditional single-field methods fail.
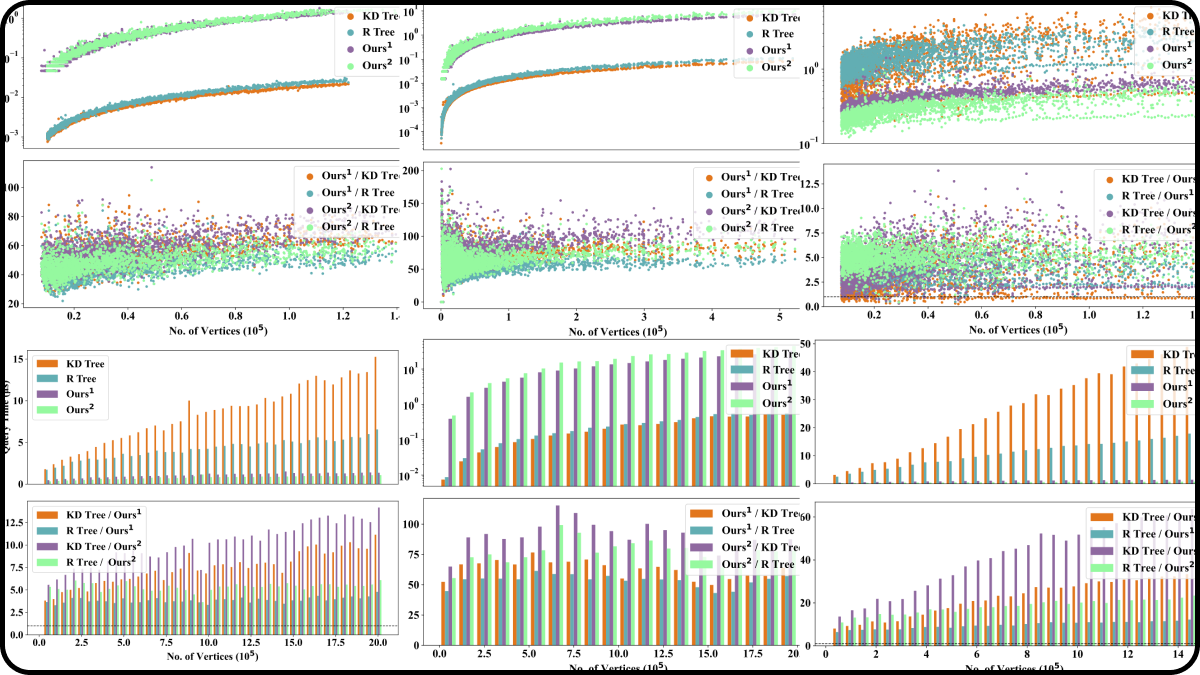
Efficient Nearest Neighbor Search Using Dynamic Programming
Pengfei Wang; Jiantao Song; Shiqing Xin; Shuangmin Chen; Changhe Tu; Wenping Wang; Jiaye Wang.
IEEE Transactions on Pattern Analysis and Machine Intelligence 2025
A novel dynamic programming framework that encodes the incremental evolution of Voronoi diagrams into a DAG to accelerate nearest neighbor search on manifolds and reduce density peak clustering complexity to $O(n \log n)$.
Efficient Nearest Neighbor Search Using Dynamic Programming
Pengfei Wang; Jiantao Song; Shiqing Xin; Shuangmin Chen; Changhe Tu; Wenping Wang; Jiaye Wang.
A novel dynamic programming framework that encodes the incremental evolution of Voronoi diagrams into a DAG to accelerate nearest neighbor search on manifolds and reduce density peak clustering complexity to $O(n \log n)$.

Toward Precise Curve Offsetting Constrained to Parametric Surfaces
Jin Zhao*; Pengfei Wang*; Shuangmin Chen; Jiong Guo; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
Computer-Aided Design (CAD). Presented at SPM 2025 2025
A novel offset computation paradigm that utilizes surface-constrained Voronoi decomposition and intrinsic triangulation to transform complex geodesic tracing into efficient, localized cell-traversal operations on parametric surfaces.
Toward Precise Curve Offsetting Constrained to Parametric Surfaces
Jin Zhao*; Pengfei Wang*; Shuangmin Chen; Jiong Guo; Shiqing Xin; Changhe Tu; Wenping Wang. (* equal contribution)
A novel offset computation paradigm that utilizes surface-constrained Voronoi decomposition and intrinsic triangulation to transform complex geodesic tracing into efficient, localized cell-traversal operations on parametric surfaces.

Towards Voronoi Diagrams of Surface Patches
Pengfei Wang; Jiantao Song; Lei Wang; Shiqing Xin; Dongming Yan; Shuangmin Chen; Changhe Tu; Wenping Wang.
IEEE Transactions on Visualization and Computer Graphics (TVCG) 2025
A high-fidelity medial axis extraction framework that generalizes Voronoi computation to 4D space via hyperplane cutting within tetrahedral elements, effectively resolving complex surface patch interactions to eliminate discretization artifacts.
Towards Voronoi Diagrams of Surface Patches
Pengfei Wang; Jiantao Song; Lei Wang; Shiqing Xin; Dongming Yan; Shuangmin Chen; Changhe Tu; Wenping Wang.
A high-fidelity medial axis extraction framework that generalizes Voronoi computation to 4D space via hyperplane cutting within tetrahedral elements, effectively resolving complex surface patch interactions to eliminate discretization artifacts.

Biharmonic Distance Driven Voronoi Diagrams Restricted on Curved Surfaces
Xuetong Zhao; Pengfei Wang; Yining Xu; Shuangmin Chen; Hui Li.
Proceedings of the International Conference on Computer-Aided Design and Computer Graphics (CAD/Graphics) 2025
A spectral geometry-based framework that integrates biharmonic embedding distances into Voronoi computation to efficiently handle thin-plate structures, preventing cross-surface penetration while enabling high-quality Centroidal Voronoi Tessellation.
Biharmonic Distance Driven Voronoi Diagrams Restricted on Curved Surfaces
Xuetong Zhao; Pengfei Wang; Yining Xu; Shuangmin Chen; Hui Li.
A spectral geometry-based framework that integrates biharmonic embedding distances into Voronoi computation to efficiently handle thin-plate structures, preventing cross-surface penetration while enabling high-quality Centroidal Voronoi Tessellation.
2024

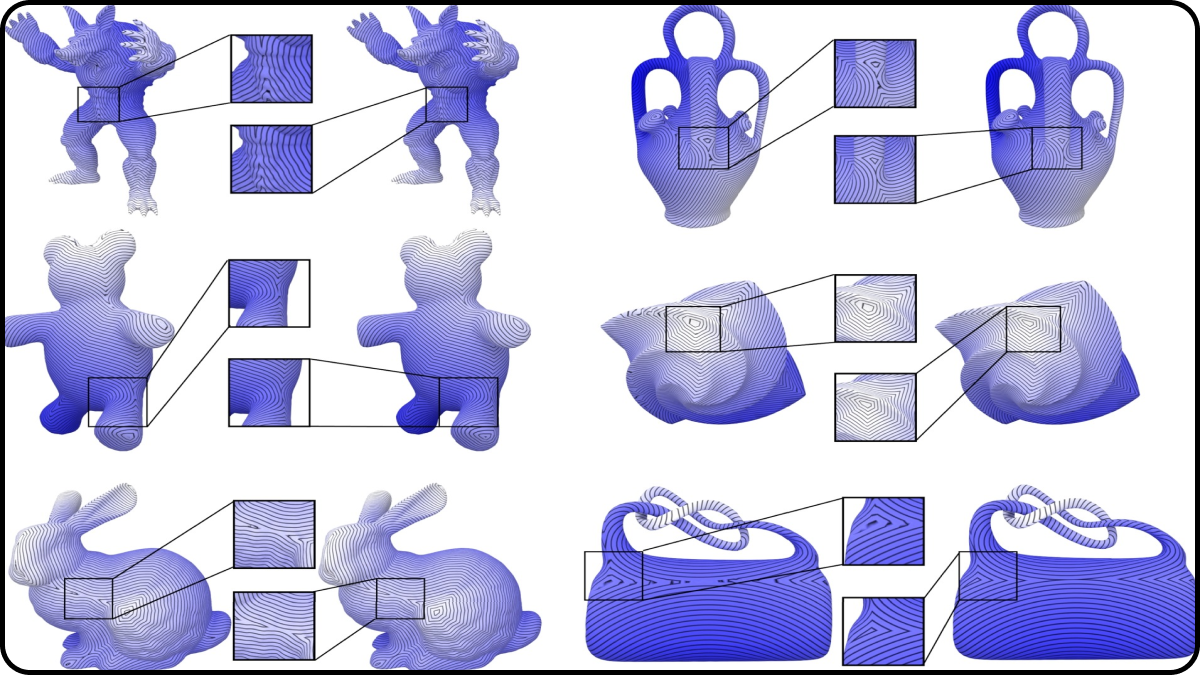
Towards geodesic ridge curve for region-wise linear representation of geodesic distance field
Wei Liu*; Pengfei Wang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Ying He; Wenping Wang. (* equal contribution)
Computer Aided Geometric Design (CAGD). Presented at GMP 2024 2024
A two-stage algorithm to compute the geodesic ridge curve on triangular meshes. By cutting the surface along the dual structure of the shortest path tree and using a fast marching solver on the extended surface, we enable accurate geodesic distance querying and high-fidelity visualization of geodesic iso-lines.
Towards geodesic ridge curve for region-wise linear representation of geodesic distance field
Wei Liu*; Pengfei Wang*; Shuangmin Chen; Shiqing Xin; Changhe Tu; Ying He; Wenping Wang. (* equal contribution)
A two-stage algorithm to compute the geodesic ridge curve on triangular meshes. By cutting the surface along the dual structure of the shortest path tree and using a fast marching solver on the extended surface, we enable accurate geodesic distance querying and high-fidelity visualization of geodesic iso-lines.

PCO: Precision-Controllable Offset Surfaces with Sharp Features
Lei Wang; Xudong Wang; Pengfei Wang; Shuangmin Chen; Shiqing Xin; Jiong Guo; Wenping Wang; Changhe Tu.
Siggraph Asia 2024 2024
A method for surface offsetting that precisely preserves sharp features by minimizing triangle-based distance fields. We employ tetrahedral space decomposition and maximal-clique formulation to simplify the offset surface complexity while maintaining high geometric fidelity.
PCO: Precision-Controllable Offset Surfaces with Sharp Features
Lei Wang; Xudong Wang; Pengfei Wang; Shuangmin Chen; Shiqing Xin; Jiong Guo; Wenping Wang; Changhe Tu.
A method for surface offsetting that precisely preserves sharp features by minimizing triangle-based distance fields. We employ tetrahedral space decomposition and maximal-clique formulation to simplify the offset surface complexity while maintaining high geometric fidelity.
2022


Efficiently Computing Voronoi Diagrams over Mesh Surfaces with Arbitrary Distance Solvers
Shiqing Xin; Pengfei Wang; Rui Xu; Dongming Yan; Shuangmin Chen; Wenping Wang; Caiming Zhang; Changhe Tu.
ACM Transactions on Graphics (TOG). Presented at SIGGRAPH Asia 2022 2022
A generalized framework for computing surface-based Voronoi diagrams that utilizes squared-distance fields to approximate arbitrary geodesic metrics, enabling efficient handling of thin-sheet models, curve generators, and constrained boundaries.
Efficiently Computing Voronoi Diagrams over Mesh Surfaces with Arbitrary Distance Solvers
Shiqing Xin; Pengfei Wang; Rui Xu; Dongming Yan; Shuangmin Chen; Wenping Wang; Caiming Zhang; Changhe Tu.
A generalized framework for computing surface-based Voronoi diagrams that utilizes squared-distance fields to approximate arbitrary geodesic metrics, enabling efficient handling of thin-sheet models, curve generators, and constrained boundaries.